3-DIMENSIONAL GRAPHS MADE FAST AND EASY
BY TOM HUDSON
PROGRAM REQUIRES 16K
In this issue of ANALOG, I review the ATARI GRAPH-IT (TM) graphics package. As you may recall, I was somewhat irritated by the rather slow nature of the "three-dimensional plot" function provided in the package. This function allows the user to generate "3D" graphs from any equation. Now, I'm not one to complain about something without offering some sort of viable alternative, so in this article I will introduce a 3-D graph program which is easy to use and will produce graphs very quickly.
By now, many readers are probably asking, "What in the world is a 3-D graph?" which is not a bad question at this point, and one which I will try to answer.
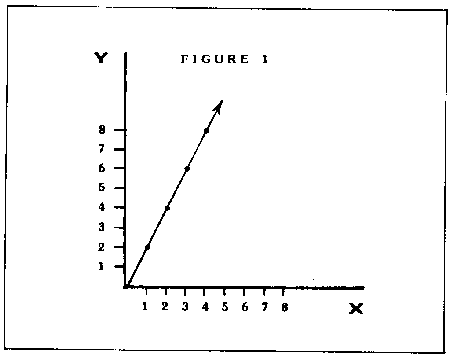
We are all familiar with the 2-dimensional (flat) graph. They are usually called "line" or "bar" graphs. Figure 1 is a line graph of the equation Y=2*X. When X is one, Y is two times one, or two. )"en X is four, Y is two times four, or eight, and so on.
In a 3-dimensional graph, things are a little more complicated. As the name implies, we are trying to represent a 3dimensional form, derived from an equation. In order to represent any 3-dimensional object, we need three coordinates. We will label these coordinates X (width), Y (depth), and Z (height).
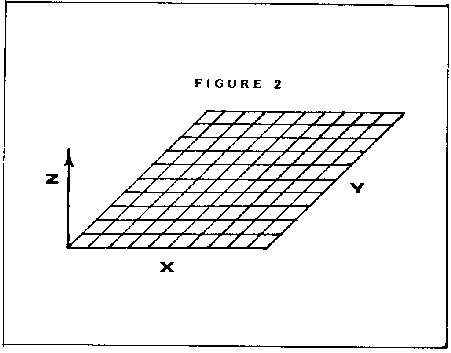
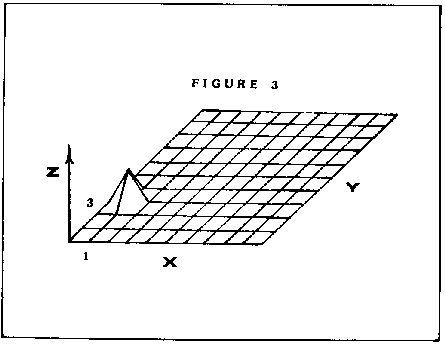
We start with a grid marked with X and Y coordinates, then we lay this grid flat, as in figure 2 (a good way to visualize this is to lay a piece of graph paper on a table in front of you). Next we use an equation to determine the 'Z' coordinate. The Z value tells how high off the table each point on the grid is. The Z coordinate is always derived from the X and Y values. For example, in the equation Z = (X+Y)*3, when we are at the coordinates X= 1 and Y =3, Z would equal 12 (4 times 3). On our graph, this would be represented as a small peak in the middle of the grid (figure 3), telling us that where X= 1 and Y=3, the Z value is 12. When this process is repeated for each point on the grid, we have a graph of the equation. 3-dimensional graphs are useful for visualizing how an equation will act with varying X and Y data.
Accompanying this article is a program listing. It is a simple but effective 3-dimensional graph generation program. It is NOT meant as a replacement for the GRAPH-IT 3D plot program but rather an enhancement.
Let's say you want a 3-D plot of an equation. You don't know what it will look like, but you'd like to get some idea before you wait an hour for GRAPHIT to process it. With this program, you can "preview" a 3-D graph, then if you want a detailed copy, you can run it through the GRAPH-IT package. An equation requiring 70 minutes on the GRAPH-IT program can be processed by this program in five. Of course, the GRAPH-IT version is much smoother and will do such things as automatic scaling, but if you need to have the output quickly, this program can do it.
| LINE# | FUNCTION |
| 80 | Set up the arrays needed to store the plot points. |
| 120 | Turn off the Direct Memory Access. This speeds up the calculations. (See ANALOG issue #2, UNLEASH THE POWER OF ATARI'S CPU) |
| 160 | Set the screen limits for the graphics clipping routine (See lines 600-720) |
| 210-230 | This is a FOR-NEXT loop for calculating the Z value for each point on the grid. Line 220 is where your equation should be placed. Line 220 in the listing is the equation that was used for the illustration above. Simply type any equation, starting with Z=. The program will do the rest. |
| 270-300 | After all the Z values have been calculated, this section changes them to plot coordinates so that they can be put on the screen. |
| 340 | This line turns the screen Direct Memory Access on again. |
| 380 | This line draws the 'zero reference' outline. This is simply the outline of the grid before the Z coordinates were calculated. It lets you know where zero is, relative to the rest of the points on the grid. |
| 420-430 | This section actually draws the grid on the screen using the data in the GX and GY arrays. It uses the graphics clipping routine (lines 600-720). The clipping routine will let the program continue drawing even if the graph goes off the screen. |
| 470-500 | These lines draw the vertical lines from the baseline to the corners of the graph. |
| 540 | This line loops the program forever. Hit the break key to stop the program. |
| 600-720 | This is a modified graphics clipping routine (See ANALOG #2, A GRAPHICS CLIPPING ROUTINE). It is modified to only clip lines that extend beyond the top and bottom of the screen, not the sides. To use, simply set up X 1, Y 1, X2 and Y2 then GOSUB 600. This is the same function as PLOT X I, Y1: DRAWTO X2, Y2. |
You can try any equation you like in line 220, just set Z to the result. Included below are a few interesting equations for you to try, along with the time required to generate the graphs. Simply replace line 220 with one of these equations. Happy graphing!
10 REM 3-D GRAPH
PROGRAM
20 REM Copyright (c) 1981
30 REM by A.N.A.L.O.G. 400/800 Mag.
40 REM WRITTEN BY TOM HUDSON
50 REM *********************
60 REM
70 GRAPHICS 24:SETCOLOR 2,0,0:COLOR 1
80 DIM GX(21,11),GY(21,11)
90 REM
100 REM *** DNA OFF ***
110 REM
120 POKE 559.0
130 REM
140 REM *** SET CLIPPING LIMITS ***
150 REM
160 XR=319:XL=0:YT=0:YB=191
170 REM
180 REM *** YOUR FORMULA GOES ***
190 REM *** INSIDE THIS LOOP ***
200 REM
210 FOR X=1 TO 21:FOR Y=1 TO 11
220 Z=(X+Y)*3
230 GY(X,Y)=Z:NEXT Y:NEXT X
240 REM
250 REM *** CALC. SCREEN COORDS. ***
260 REM
270 FOR X=1 TO 21:FOR Y=1 TO 11
1-80 GX(X,Y)=(X-1)*10+(Y-1)*10
290 GY(X,Y)=180-(Y-1)*10-GY(X,Y)
300 NEXT Y:NEXT X
-7,10 REM
320 REM *** DNA ON AGAIN ***
330 REM
340 POKE 559,34
350 REM
360 REM *** DRAW BASELINE ***
370 REM
380 PLOT 0,180:DRAWTO 200,180:DRAWTO 3
00,80:DRAWTO 100,80:DRAWTO 0,180
390 REM
400 REM *** PLOT THE GRAPH ***
410 REM
420 FOR X=1 TO 21:FOR Y=2 TO 11:X1=GX(
X,Y-1):Y1=GY(X,Y-1):X2=GX(X,Y):Y2=GY(X
,Y):GOSUB 600:NEXT Y:NEXT X
430 FOR Y=1 TO 11:FOR X=2 TO 21:X1=GX(
X-1,Y):Y1=GY(X-1,Y):X2=GX(X,Y):Y2=GY(X
,Y):GOSUB 600:NEXT X:NEXT Y
440 REM
450 REM *** DRAW VERTICAL LINES ***
460 REM
470 X1=0:Y1=180:X2=GX(1,1):Y2=GY(1,1):
GOSUB 600
480 X1=200:Y1=180:X2=GX(21,1):Y2=GY(21
,1):GOSUB 600
490 X1=300:Y1=80:X2=GX(21.11):Y2=GY(21
,11):GOSUB 600
500 X1=100:Y1=80:X2=GX(1,11):Y2=GY(1,1
1):GOSUB 600
510 REM
520 REM *** LOOP FOREVER ***
530 REM
540 G0TO 540
550 REM
560 REM *************************
570 REM * GRAPHICS CLIP ROUTINE *
580 REM *************************
590 REM
600 T1=0:T2=0:B1=0:B2=0:IF Y1<YT THEN
T1=1:GOTO 620
610 IF Y1>YB THEN B1=1
620 IF Y2<YT THEN T2=1:GOTO 640
630 IF Y2>YB THEN B2=1
640 IF T1+T2=2 OR B1+B2=2 THEN RETURN
650 X3=X1:Y3=Y1:X4=X2;Y4=Y2;GOSUB 690
660 T1=T2:B1=B2:X1=XW:Y1=YW:X3=X2:Y3=Y
2:X4=X1:Y4=Y1:GOSUB 690
670 IF Y1<YT OR Y1>YB OR YW<YT OR YW>Y
B THEN RETURN
680 PLOT X1,Y1:DRAWTO XW,YW:RETURN
690 IF T1+B1=0 THEN XW=X3:YW=Y3:RETURN
700 IF T1 THEN YW=YT:XW=X3+(X4-X3)*(YT
-Y3)/(Y4-Y-!-'):X3=XW:Y3=YW:RETURN
710 IF B1 THEN YW=YB:XW=X3+(X4-X3)*(YB
-Y3)/(Y4-Y3):X3=XW:Y3=YW:RETURN
720 RETURN